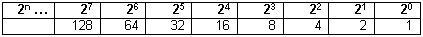
Mindennapjainkban tízes számrendszert használunk, de a számítógép működése alapvetően a kettes számrendszerre épül. A kettes számrendszerben történő számábrázolás nehézsége miatt gyakran alkalmazzák a tizenhatos számrendszerbeli számábrázolást is.

Ismerkedjünk meg a különböző számrendszerekben történő számolás módjával!

A számrendszerek a valós számok ábrázolására szolgáló jelek és alkalmazásukra vonatkozó szabályok összessége. Minden számjegypozícióhoz egy helyi értéket rendelünk, és a valós szám értékét az egyes helyi értékek és a hozzájuk tartozó értékek szorzatainak összege adja. A mennyiségeket a számrendszer alapjának hatványaival írjuk fel, ahol a számrendszer alapja bármely 1-nél nagyobb egész szám lehet.

Amivel foglalkozunk:

• Tízes (decimális) számrendszer
• Kettes (bináris) számrendszer
•   º Átváltás decimális számrendszerből bináris számrendszerbe
•   º Átváltás bináris számrendszerből decimális számrendszerbe
• Tizenhatos (hexadecimális) számrendszer
•   º Átváltás decimális számrendszerből hexadecimális számrendszerbe
•   º Átváltás hexadecimális számrendszerből decimális számrendszerbe
•   º Átváltás bináris számrendszerből hexadecimális számrendszerbe
•   º Átváltás hexadecimális számrendszerből bináris számrendszerbe
• Értéktáblázat

▲ Lap tetejére

Tízes (decimális) számrendszer 

A tízes számrendszerben a számokat a tíz hatványaival ábrázoljuk. Lássunk egy példát!

A 2532 tízes számrendszerbeli számot az alábbi formában írhatjuk fel:

103	102	101	100
2	5	3	2

Ennek az értékét a következő módon számíthatjuk ki:

2 x 10³ + 5 x 10² + 3 x 10¹ + 2 x 10⁰ =
2 x 1000 + 5 x 100 + 3 x 10 + 2 x 1 =
2000 + 500 + 30 + 2 =
2532

▲ Lap tetejére

Kettes (bináris) számrendszer 

A kettes vagy más néven bináris számrendszerbeli számok a 0 és az 1 számjegyekből állnak. A számjegyek helyiértékeit az alábbi táblázatban foglaltuk össze.

• Átváltás decimális számrendszerből bináris számrendszerbe: 

A számítógépen leggyakrabban nyolc számjegyből álló bináris számokkal találkozhatunk. A nyolc számjegyen ábrázolható legnagyobb érték a 255=(128+64+32+16+8+4+2+1)

A tízes (decimális) számrendszerbeli számokat kettővel való maradékos osztással tudjuk a legegyszerűbben bináris számrendszerbeli számmá alakítani

Az átalakítandó számot osszuk el kettővel. Minden osztásnál jegyezzük fel a maradékot. Folytassuk az egészrésszel való osztást, amíg nullát nem kapunk

Lássunk erre egy példát! Az átváltandó szám: 81₁₀.

Az így kapott maradékokat lentről felfelé olvasva kapjuk meg a bináris számot: 1010001₂.

• Átváltás bináris számrendszerből decimális számrendszerbe: 

A bináris számrendszerbeli számokat úgy válthatjuk át decimális számrendszerbe, hogy a bináris szám egyes számjegyeit megszorozzuk a hozzájuk tartozó helyiértékekkel, majd az így kapott értékeket összeadjuk.

Például az 10001011₂ bináris szám decimális értékét az alábbi módon számíthatjuk ki:

▲ Lap tetejére

Tizenhatos (hexadecimális) számrendszer 

A tizenhatos vagy más néven hexadecimális számrendszerbeli számok 0 és 15 közötti helyi értékeket tartalmazhatnak, melyek a következők: 0 1 2 3 4 5 6 7 8 9 A B C D E F

Az egyes betűk a következő értékeket szimbolizálják:

A=10, B=11, C=12, D=13, E=14, F=15

• Átváltás decimális számrendszerből hexadecimális számrendszerbe: 

A decimális számrendszerbeli számokat tizenhattal való maradékos osztással tudjuk hexadecimális számrendszerbeli számmá alakítani.

Az átalakítandó számot osszuk el tizenhattal. Minden osztásnál jegyezzük fel a maradékot. Folytassuk az egészrésszel való osztást, amíg nullát nem kapunk. Figyeljünk arra, hogy 10-től felfelé az értékeket betűkkel jelöljük!

Lássunk erre egy példát! Az átalakítandó szám: 1015₁₀.

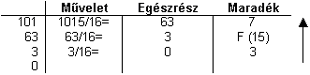
Az így kapott maradékokat lentről felfelé olvasva kapjuk meg a hexadecimális számot: 3F7₁₆.

• Átváltás hexadecimális számrendszerből decimális számrendszerbe: 

A hexadecimális számrendszerbeli számokat úgy válthatjuk át decimális számrendszerbe, hogy a hexadecimális szám egyes számjegyeit megszorozzuk a hozzájuk tartozó helyi értékekkel, majd az így kapott értékeket összeadjuk.

Például az A5₁₆ hexadecimális szám decimális értékét az alábbi módon számíthatjuk ki.

• Átváltás bináris számrendszerből hexadecimális számrendszerbe: 

Bináris számrendszerből hexadecimális számrendszerbe történő átváltáskor a bináris szám számjegyeit osszuk a szám utolsó számjegyétől kezdve négyes csoportokra. Ha az első csoportban négynél kevesebb számjegy szerepel, az első számjegy elé annyi nullát írjunk, hogy négy számjegyet kapjunk. Számítsuk ki az egyes csoportok értékeit, majd az így kapott számokat váltsuk át hexadecimális számjegyekké és olvassuk össze.

Lássunk egy példát! Az átváltandó szám az 10111111001₂.

A táblázat utolsó sorát balról jobbra összeolvasva az eredmény tehát: 5F9₁₆

• Átváltás hexadecimális számrendszerből bináris számrendszerbe: 

A hexadecimális számrendszerbeli számok bináris számrendszerbeli számmá történő átalakításához első lépésként váltsuk át a hexadecimális számjegyeket decimális számokká. Az így kapott értékeket váltsuk át bináris számokká, majd az eredményt olvassuk össze.

Lássunk egy példát! Az átváltandó szám a 7BA₁₆

A táblázat utolsó sorát balról jobbra összeolvasva az eredmény tehát: 11110111010₂

Értéktáblázat
 

▲ Lap tetejére